持久化数据结构简介

这篇文章是系列文章的一部分，如果还没有浏览过文章的其它部分请参考：

作为系列博客的第一篇，这篇博客将会先给出一些持久化数据结构的简介并以最简单的 List （列表）数据结构为例，介绍一些常见的持久化数据结构实现方法。这一个系列的文章都主要参考了 Understanding Persistent Vector 这篇非常经典的文章，其中一些章节甚至可以看作是对它内容的翻译。建议有兴趣的读者浏览原文作为参考。

持久化数据结构简介

持久化(Persistent)数据结构又叫不可变(Immutable)数据结构，顾名思义，这类数据结构的内容是不可变的。也就是说，对于这类数据结构的修改操作，都会返回一个新的副本，而原来的数据结构保存的内容不会有任何改变。这样的数据结构是有意义的，比方说我们现在所编写的所有程序，都可以看作是一个状态机，也就是说在程序运行的过程的每一个时刻，程序本身可以被看作存在一个状态(State)，我们的语句作用在当前状态上，从而不断地产生出进一步的状态，由此循环往复。如果按照这样的模型，那么就存在两个可能的问题需要解决：

我们的有些行为可以看作一系列对状态的修改，比如说通过一个函数内的一系列操作来实现一个功能，先读出数据库里的内容来进行修改等。这时，我们希望这一连串操作是原子的。也就是说整个过程要么全部成功，要么全部失败。这样的要求在数据库里是通过事务(Transaction)来实现的，某些编程语言(如Haskell)也提供了类似的方案，而持久化数据结构也是解决这一问题的一种方法——将原来的状态保存在不可变的数据结构中，只有当整个操作成功完成再将生成的新状态替换回去，这样系统就不会进入过程错误导致的中间状态。
在并发程序中，一个函数的执行可能会带有副作用——同样的输入和函数，得到的返回结果却可能不一样。比方说，将一个数组传递进一个函数进行遍历处理，在函数执行的过程中，另一个线程修改了数组的内容，这样就产生的线程同步等复杂的问题，增加了程序出现问题的可能性，也增加了 Debug 的难度。由于持久化数据结构本身不会被修改，因此将它传入一个函数是安全的，任何对他的修改都表现在一个新的对象上，因此你传入函数的输出并不会被影响。

有些数据结构的实现为了在并发条件下安全运行，比如使用一些方法为数据结构加锁，这一行为实际上会增加数据结构实现的难度和运行性能，持久化数据结构不会改变原来的状态，自然也就不会有加锁的必要。事实上，持久化数据结构天生是一种无锁的数据结构。

当然，持久化数据结构也有一些缺陷，主要体现在以下几个方面：

由于持久化数据结构在修改时需要生成新的对象，因此往往会比普通数据结构更加耗费内存空间。因此，任何持久化数据结构在设计上都要考虑如何节省空间这一问题
持久化数据结构往往是在原始数据结构上的包装，通过更复杂的操作保证原始数据结构的数据的不变性，这不但体现在修改操作上，也体现在读取操作上。因此持久化数据结构的读写速度往往会慢于普通数据结构，其实现也更复杂
持久化数据结构脱胎于函数式编程，与一般的过程式编程语言在思维模式上差别比较大，操作起来也有很大不同，因此对于习惯了传统过程式编程语言的学习者来说接受起来有一定的困难

尽管如此，持久化数据结构仍然有很大的应用空间，下面给出它们的一些应用场景。

持久化数据结构的应用

持久化数据结构在很多情况下是有优势的，虽然大部分数据库帮我们实现了事务模型，让我们可以安全放心的使用，但是在大多数其他软件系统中并没有现成的事务工具供我们使用，事务模型依赖于对数据操作的记录，如果运行失败需要对状态进行 Rollback，这不但是一个很难实现的功能， Rollback 过程也需要花费不少时间。相比起来持久化数据结构就成了一种更容易获得的选择。实际上，除去 Clojure、Scala 等这种自带了持久化数据结构的编程语言，绝大部分编程语言都有成熟可靠的开源库提供了此类数据结构。

在 React + Flux 模型中，不可变数据结构还被用来加速状态改变的对比，因为 React 依赖于对比前后两个状态之间的改变来发现需要对 Virtual DOM 进行的最小改变，因此必须要保留每一次修改之后的状态。所有的操作都必须通过setState方法进行，很难保证之前的状态没有被其他地方意外的修改，而对比本身也是耗时的。但是在引入ImmutableJS后，每个 View 的状态就可以很安全的保存起来了。由于在 React 里，state 改变总是从一个最初的状态衍生而来的一系列状态，在对前后两个状态进行递归的比较时，如果两个对象的引用是一样的，那么它们一定是一个不可变的对象，如果两个对象的引用不一致，那么一定经过了修改。因此通过这样的优化可以加速比较的过程。

持久化数据结构的另一个应用是实现文件系统的 Copy on Write 功能，很多文件系统以及虚拟机(VirtualBox)和容器(Docker) 都提供 Snapshot 的功能，也就是说你可以保存文件系统在某一时刻的完整状态并在未来某个时间方便地恢复到当前状态。这在部署服务的时候非常有用——如果新上线的系统出现问题，我们可以快速简单地回复到原来正常的状态。传统的 CoW 实现是在某一文件修改的过程时候再复制它，这种实现在遇到比较大的文件时是比较浪费空间的。然而很多持久化数据结构的实现本身就考虑到了节省空间的问题，因此可以很大程度上缓解这一问题。也就是说，对于一个文件，我们可以只在写入的时候复制其中一小部分来实现块级别的 CoW。在接下来的文章中我们可以看到，Vector trie 这种数据结构就很适合实现这一功能。

持久化数据结构的最广泛的应用还是在并发编程当中，结合函数式编程的模型实现高性能且安全易于预测的代码编写。在一些多人联机系统(协作工具、联机游戏)当中，多个用户会并发地对某一个中心的状态进行修改，而这个中心状态还需要定期的保存。使用不可变数据结构，每一个被传入的状态都是当时状态的不可变的快照，因此我们可以安全的在一个新的线程上执行保存操作。这提高了我们程序的并发性。

持久化数据结构的实现

在介绍了持久化数据结构的特点和应用之后，我们以最简单的顺序储存结构 List (列表)为例，从简入繁介绍几种实现不可变数据结构的方法和思路。

首先，我们把 List 定义为一种顺序储存结构，它所保存的元素从 0 开始编号，依次向后储存。这一储存结构包含如下几种基础的操作：

New 新建一个 List
Get(index) 获得指定 Index 的元素
Set(index, value) 修改指定 Index 的元素
PushBack(value) 在 List 末尾添加一个元素
RemoveBack(value) 从 List 末尾去除一个元素

此外，这个 List 可能还可以支持如下的一些操作，它们都可以用上面方法来实现(尽管有些数据结构支持更直接的方法)：

Insert(index, value) 在指定位置插入一个元素
Remove(index, value) 在指定位置删除一个元素
Slice(i, j) 获得 List 当中 i 到 j 之间元素的一个切片
Splice(i, j, List) 将 List 当中 i 到 j 之间的元素替换为传入的 List 当中的元素

在实现持久化数据结构的过程中，我们主要考虑的问题是每一种操作的时间消耗和数据结构的空间效率。我们的目标自然是寻找一种在空间和时间上都比较有效的解决方案，然而也需要注意到各种不同的思路都有比较适合的使用场景，并不存在在各种情况下都最佳的实现。

在讨论的过程中，除了使用大 O 表示法来衡量数据结构的时间效率，还使用数据元素所占空间除以数据结构使用的总空间所得的比例来衡量数据结构的空间效率。

数组

数组是最简单的线性储存结构了，它在 C++ 中是 vector ，在 Java 中是 ArrayList，在 Golang 中则是 slice。数组本质上是一段连续的内存空间，数据元素一个接着一个的摆放。

一般来讲，数组在创建时会预先分配一部分空间，当PushBack操作用完已经分配的所有空间之后，需要分配一块大小为原来 2 倍(Java 中是 1.5 倍)的空间，再将原来的数据拷贝过来。显然，在现今的内存模型中，对于数组元素进行 Get 和 Set 操作的时间复杂度都是 O(1)O(1)O(1) 的，也就是说数组数据结构特别适合随机访问。尽管在空间耗尽的时候需要进行空间倍增和复制的操作，但是均摊下来，每次 PushBack 操作的时间复杂度也是 O(1)O(1)O(1) 的。

尽管看起来倍增操作让数组比较浪费空间，但是实际情况下数组数据结构是空间利用率最高的数据结构之一，譬如说对于 Java 来说，平均的空间效率是 75% 。

这些特点使得数组成为最常用的数据结构之一，它同时也是一些其他数据结构(如 Hash 表)的基础。但是对于数组来说， Insert、Remove 和 Splice 操作的时间复杂度都比较高(O(N)O(N)O(N))。数组的另一个缺点在于如果数据量较大，倍增时需要分配非常大的空间可能是比较困难的。

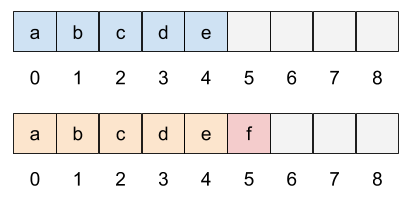
数组作为我们通向持久化数据结构的引子，其本身并非一个合适的选择——如下图所示，如果我们要保证每次修改时原来的数据不会被修改，唯一的办法是将所有的数据复制一遍。接下来我们可以看到，在数组基础上进行的一些改进将有助于解决这一问题。

ArrayList

链表

上面我们提到过，数组类型的数据结构一个比较大的问题就是需要分配大块连续的空间，这在内存比较紧张的环境下可能比较困难，另外一个巨大的缺点在于由于数组是必须是连续的空间，导致如果我们想在它的基础上实现持久化数据结构比较困难。

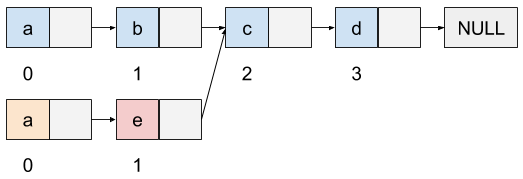
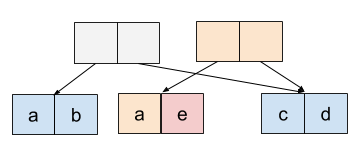
一种解决方案是链表，链表的特点是将储存的每个数据拆开来存放，对于简单的单链表来说，每一个数据单元包括一个数据字段和一个指针字段。每个指针指向当前单元的下一个单元或者 NULL 代表链表的结束。如果使用链表结构，Get 和 Set 的平均时间复杂度都是 O(N)O(N)O(N)，尽管如此，在末尾插入和删除数据的 PushBack 和 RemoveBack 可以实现为 O(1)O(1)O(1)。实际上，链表特别适合这种频繁在头部和尾部进行增删操作的使用场景，因此特别适合作为队列或者栈。如果将链表作为顺序储存结构，那么在进行数据修改的时候，我们可以复用所有当前修改之后的数据单元，如下图所示，我们将第二个单元的数据 b 改为 e ，只需要将其之前的 a 所在的单元也复制一遍，由此节省了不少空间。

LinkedList

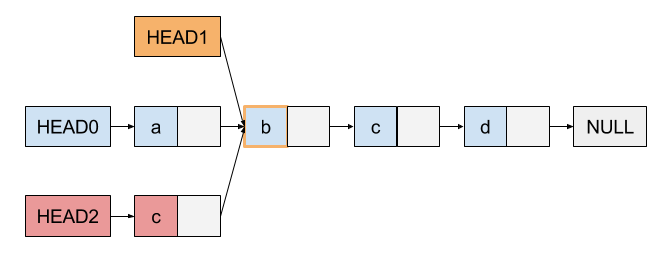
实际上，链表实现的栈是持久化栈实现的理想数据结构，假定我们保留一个指向栈顶的HEAD指针，那么当我们在栈中进行Push 和Pop操作的时候，只需要复制HEAD指针以及修改指向的位置即可，下图的HEAD0、HEAD1、HEAD2分别代表原始栈、 Pop一次、Push一次之后整个栈的结构关系。可以看到，只要我们记录下操作过程中的HEAD，就可以获得对应状态的一个快照，这些快照本身不知晓其他快照的存在，但是却共享了大部分空间。

LinkedStack

然而链表作为一种顺序储存结构，其缺点也是很明显的。首先就是对随机数据访问的支持较差，每次访问一个数据单元，都要遍历之前所有的单元，此外链表的空间效率也很低——由于每个数据单元必定至少包含一个指针字段，链表的数据效率根本无法超过 50% 。

串

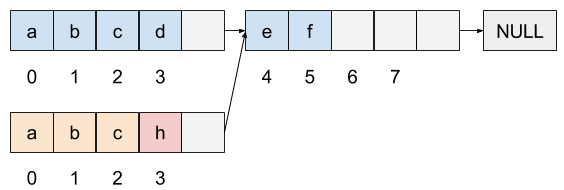
为了解决链表存在的问题，一个很自然的想法就是增加一个数据单元当中数据字段本身所占有的比例，这就是串的实现原理：在每个结构体当中用一个固定长度的数组储存数据。这样的做法不但增加了空间效率，也提高了PushBack操作的时间效率。使用串，在每次之前分配的空间用完的时候，只需要分配一个相对较小的新的数据单元，而不需要像数组那样倍增并复制所有的数据。串可以看作数组和链表相结合所产生的数据结构，它具有很不错的顺序访问性能，特别是串的长度恰好可以被放进 CPU 的 Cache 当中时它不会像链表那样需要频繁从内存调入下一个单元。用串实现持久化数据结构的时候，需要将所修改数据所在单元以及之前的数据都复制一遍，稍稍比链表更冗余一些，但是由于串本身的空间效率很高，所以实际上还是非常划算的。

String

串在实际生活中的应用不少，比如早期 Windows 的文件系统 FAT32 和 NTFS，每个文件在磁盘上就是组织为一块块数据组成的串，但是串跟链表的缺点很像，它们都缺乏随机访问数据的能力。有没有一种数据结构能在Get、Set、PushBack和RemoveBack 上都表现出相当好的时间效率呢？其中一种常见的解决方案是平衡树。

平衡树

平衡树是一系列数据结构的统称，它包括各种平衡二叉树，如 AVL 树、红黑树等，也包括常用的多叉平衡树如 B+ 树、 B- 树等。由于这些基本的数据结构不是本文的重点，本文不会对其具体实现进行逐个详细的介绍，如下是一棵红黑树的示例。

Red Black Tree

以平衡二叉为例，一般的二叉树都可以保证Get、Set、Insert 和 Remove 等操作具备 O(logN)O(log⁡N)O(\log N) 的最差时间复杂度，在很多情况下已经非常优秀，最重要的一点是一些平衡二叉树每次操作最多修改 O(logN)O(log⁡N)O(\log N) 个内部节点。这启发我们，如果我们把所有这些修改节点的操作变为复制，那么就能在不改变原来数据的情况下，获得新的数据的一个快照！使用这种方式，我们可以在没有明显时间效率损失的情况下极大程度地复用原来空间。

事实上，平衡树确实是非常流行的持久化数据结构实现方案，在很多情况下它的时间效率都令人满意。然而，平衡树的空间效率相当低下，拿一般的平衡二叉树来说，每个数据节点至少包含一个数据字段和两个指针字段，还可能需要其他字段储存信息以便于获得快速平衡二叉树的能力，因此它们的空间效率一般最多在 30% 左右，在有些情况下并不能让人满意。

Vector trie

终于来到了我们要介绍的重点: Vector trie 。Vector trie 可以看作将前述的几种数据结构的思路相结合的产物，首先我们可以观察到如下两点：

串数据结构虽然具有较好的空间效率，但是却缺乏随机访问的时间效率
树数据结构虽然有较好的操作性能，但是空间效率和顺序访问的时间效率较差

那么如果我们将两种数据结构结合起来是否能构造一个在两方面都表现优秀的数据结构呢？答案是肯定的。将两种数据结构结合起来的是一种新的数据结构 trie (前缀树)。关于前缀树的特点这里不再赘述，不了解的读者可以先查询 Wikipedia 上的介绍。下图是一个 Vector trie 的示意图。

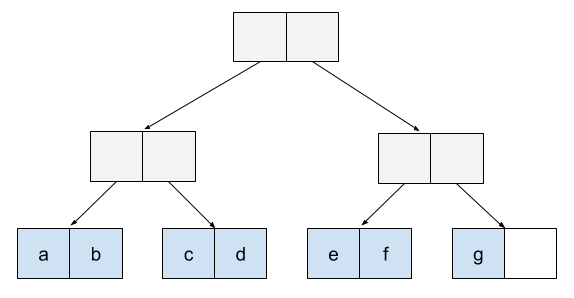
Vector Trie

可以看到，在这种数据结构当中，所有的数据都保存在树的叶子节点，因此树的最下一层叶子节点实际上可以被看成是串，唯一的区别是，不同于串使用末尾的指针指向下一个数据单元，Vector trie 使用 Trie 树结构作为每个数据节点的索引。在 Vector trie 当中，每次检索都从根开始，依次经过多个中间节点到达叶子节点并获得数据。

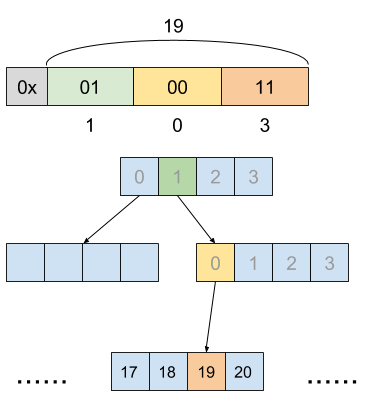
在实际使用中，一个内部节点的子节点被组织成数组，那么我们就可以方便地使用 Index 二进制作为 Trie 查询的依据，以一个固定宽度的窗口依次获得应该由当前节点进入哪个子节点。如下图所示，我们以两位为单位，依次由根访问到叶子节点，最终到达目的数据所在的位置 (为简便起见，大多数 Trie 节点被省略)。

Trie Traverse

在第一张图中我们使用的每个内部节点有两个孩子节点，因此实际上退化成了二叉树，这样几个基本操作的时间复杂度都在 O(logN)O(log⁡N)O(\log N)。在实际实现中，Vector trie 一般使用有 32 个分支的内部节点，整个树的结构更加扁平化，操作的时间效率也更高——一般来说为 O(log32N)O(log32⁡N)O(\log_{32} N)，考虑到一般的顺序储存结构的最大容量只有 2322322^{32}，因此在 Vector trie 上进行的各项操作的时间复杂度可以认为是 O(7)O(7)O(7) 也就是常数时间的的操作。当然，O(log32N)≠O(1)O(log32⁡N)≠O(1)O(\log_{32} N) \neq O(1)，但是很多 Vector trie 的实现为了宣传的目的，都自诩为常数时间的时间复杂度，这也给初学者造成了一定的困惑。

下图揭示了 Vector trie 如何实现持久化，和一般的树结构一样，每次修改操作的时候，我们复制从根到叶子节点的路径而不是直接修改它们，这样从两个根我们就可以访问到对数据不同时刻的两个快照。

Immutable VectorTrie

Vector trie 实现持久化数据结构的基本原理由此就介绍清楚了，但是在实际为了进一步进行性能的优化还会做一些诸如 Tail 节点、Transient 实现等优化，这些内容将会留在以后进一步介绍。

那么 Vector trie 的时间和空间效率如何？根据 Persistent Vector Performance 这篇博客的介绍，对于 Get，Set 等操作，Vector trie 确实跟一般宣传的相似，相比简单的 Array 只有一个接近常数级别的放大。而如果利用 Transient 优化，在PushBack等操作上甚至有超越 Array 的趋势。更进一步，经过 Benchmark 所选择的 32 这个分支系数，也让 Vector trie 可以在常见 CPU 结构的 Cache 系统中表现出优异的顺序访问性能。另一方面，在空间使用上 Vector trie 平均有一个接近甚至超过 90% 的空间效率，令人十分印象深刻。由此可见 Vector trie 是一种理想的用于实现持久化的数据结构。

实际上，包括 Clojure、Scala 在内的多种编程语言都选择了这种数据结构作为持久化数组的实现。同样， Vector trie 的索引结构也很接近一些文件系统对文件的索引结构，因此也就可以方便的被应用于实现文件系统的 Snapshot 和 Copy on Write 功能。

Vector trie 和普通的 Array 一样，在 Insert、Splice 等操作上时间效率很低，这是它主要的问题之一。

总结

本文介绍了函数式编程中常见的持久化数据结构的优点和常见应用，并以持久化数组为例，逐步探讨了几种实现思路。其中 LinkedList 很适合用来实现持久化栈，而平衡树和 Vector trie 在实现持久化数组上各有优势。我们最后选择了 Vector trie 做为我们将要使用 Golang 实现的对象。

当然，常用来实现持久化数据结构的方法不仅限于这些，本文尚未涉及到的一种更高级的数据结构是 Finger Tree，这种数据结构在 Haskell 编程语言的部分库中得到了应用。

按照计划，下一篇博客将会介绍不带持久化功能的 Vector trie 的简单实现过程，再之后将会给出 vector trie 实现持久化功能的过程并介绍 Transient 的实现原理。

敬请期待。

菜单

持久化数据结构简介